Keeping Time By The Sun

Posted on May 24, 2013 by Jack Case

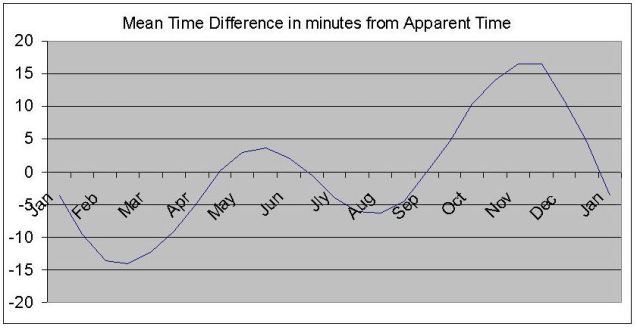
The True Sun.  Life on Earth is governed by the movement of the True Sun; that is the sun we see in the sky and not by the theoretical Mean Sun.  The units of time in everyday use are defined in terms of the True Sun and are known as Apparent Solar Time.

The Sun as a Time-Keeper.  Because the Earth’s orbital motion is not uniform, there are corresponding variations in the apparent speed of the Sun along the ecliptic.   For this reason, the hour angle of the True Sun does not increase at a uniform rate and therefore does not give an accurate measurement of time.  To overcome this problem without losing the connection with the True Sun, the Mean Sun (as defined below) is used.

The Mean Sun is an imaginary body which is assumed to move in the celestial equator at a uniform speed round the Earth and to complete one revolution in the time taken by the True Sun to complete one revolution of the ecliptic.

 The Mean Solar Day is the time taken for the Mean Sun to make one complete circuit of the Earth.  In other words, it is the time taken for the Mean Sun to transit all 360 meridians of longitude.  The time system based on the Mean Solar Day is known as Mean Solar Time.

Apparent Noon is when the True Sun is on an observer’s meridian of longitude.  It is when the Sun reaches its greatest altitude above the observer’s horizon.  In other words it is when the Sun is at its zenith.

Mean Noon occurs when the meridian of the Mean Sun coincides with the meridian of a place.

Local Mean Time (LMT) is the local hour angle of the Mean Sun measured westwards from the meridian of a certain place and expressed in terms of time instead of arc.

Greenwich Mean Time (GMT) is the local mean time anywhere on the meridian of Greenwich.  In other words it is the Local Hour Angle of the Mean Sun on the meridian of Greenwich.  Since the Greenwich meridian is used as the base meridian from which the longitude of all places on Earth are identified, it provides the link between the LMT of a place and the LMT at Greenwich (or GMT).

Standard Time.  For each place on Earth to keep its own local mean time would obviously cause a great deal of confusion and difficulty.  For this reason, Standard Time is introduced so that places in the same locality can keep the same time.  The time chosen is usually based on a convenient meridian running through the area and the meridian chosen usually differs from the Greenwich meridian by a whole number of hours.  Some large countries, such as the U.S.A. have several different standard times.

Zone Time (ZT).  It would be impossible for a ship at sea to keep to the time of its longitude because (unless it is travelling due north or south) the longitude will be constantly changing.  For this reason, the sea areas of the Earth are divided into time zones which are 15o of longitude (or 1 hour) apart.   The central meridian of each zone is an exact number of hours distant from the Greenwich meridian so that zone time differs from GMT by multiples of 1 hour.  The time kept in each zone is the time of its central meridian and is plus or minus GMT depending on the zone’s position east or west of Greenwich.

Time Zone System.  The Earth is divided into 24 zones of 15o of longitude each, with the centre of the system being the Greenwich meridian.  Therefore, the centre zone (zone 0) lies between 7.5o W. and 7.5o E.   The zones lying to the West of Greenwich are numbered from +1 to +12 and those to the East from -1 to 12.  The 12th zone is divided by the meridian 180o which is known as the International Date Line.  The two halves of the 12th zone are marked + or – depending on which side of the date line they lie.

Time difference between meridians of longitude.

We know that the Earth revolves about its axis once every 24 hours.  In other words, the Sun completes its apparent revolution of 360o in 24 hours.  This means that the Sun crosses each of the 360 meridians of longitude once every 24 hours.   So, in 1 hour, the Sun appears to move 15o,

in 4 minutes, it appears to move 1o,

in 1 minute it appears to move 15′,

in 4 seconds it appears to move 1′.

Declination.  The Declination of a celestial body is its angular distance North or South of the Celestial Equator.  The declinations of the stars change very slowly and can be considered to be almost constant for up to a month at a time.  The declination of the Sun, on the other hand, changes relatively fast from 23.5o North to 23.5o South and back again during the course of a year.

Declination can be summarised as the celestial equivalent of Latitude since it is the angular distance of a celestial body North or South of the Celestial Equator.

The Equinoxes.  The Sun crosses the celestial equator on two occasions during the course of a year and these occasions are known as the equinoxes.  At the equinoxes, at all places on Earth, the nights and days are of equal duration (i.e. 12 hours) hence the term equinoxes (equal nights).  Because the Sun is on the celestial equator at the equinoxes, its declination is of course 0o.

 The Autumnal Equinox occurs on about the 22nd.September when the Sun crosses the celestial equator as it moves southwards from 23.5oN , the northernmost limit of its declination.

The Vernal Equinox occurs on about the 20th.March when the Sun crosses the celestial equator as it moves northwards from 23.5oS, the southernmost limit of its declination.

The Solstices.  The times when the Sun reaches the limits of its path of declination are known as the solstices.  The word solstice is taken from ‘solstitium’, the latin for ‘sun stands still’.  This is because the apparent movement of the Sun seems to stop before it changes direction

The Summer Solstice (mid-summer in the northern hemisphere) occurs on about 21st. June when the Sun’s declination reaches 23.5o North (the tropic of Cancer).

The Winter Solstice (mid-winter in the northern hemisphere) occurs on about 21st. December when the Sun’s declination is 23.5oSouth (the tropic of Capricorn).

The Autumnal Equinox occurs on about the 22nd.September when the Sun crosses the celestial equator as it moves southwards from 23.5oN , the northernmost limit of its declination.

The Vernal Equinox occurs on about the 20th.March when the Sun crosses the celestial equator as it moves northwards from 23.5oS, the southernmost limit of its declination.

Note.  The latitude of the tropic of Cancer is currently drifting south at approximately 0.5’’ per year while the latitude of the tropic of Capricorn is drifting north at the same rate.

Note.  It has only been possible to give a brief explanation of this topic here.  A fuller exposition is given in the book Astro Navigation Demystified.

Other links:

Survival Sundial

Equation of Time

Sidereal Time

Local Hour Angle

Relationship Between Longitude and Time

web:  astronavigationdemistified.com

Posted in Uncategorized | Tagged , , , , | Leave a comment

Is Venus an Evening Star or a Morning Star?

Posted on May 16, 2013 by Jack Case

Venus sometimes appears as an evening star above the western horizon shortly after sunset and sometimes appears as a morning star above the eastern horizon shortly before sunrise.  In primitive times, people regarded the evening and morning stars as two different heavenly bodies but in the sixth century BC, Pythagoras suggested that they might be one and the same body.

Ptolemy believed that the Earth was the centre of the Universe and that the Sun moved in a circular orbit around the Earth which was stationary.  He also believed that Venus orbited the Sun as the Sun itself orbited the Earth and that this explained why Venus appeared from Earth as an evening star during part of its orbit and as a morning star during another part. The Ptolemaic hypothesis can be explained with the aid of diagram 1 below:

venus1 amend

According to the Ptolemy, if Venus were at a point in its orbit somewhere on the semicircle ABC, say at B, then the line joining the Earth to Venus would be to the left of the line joining the Earth to the Sun.  Therefore, looking from Earth, Venus would appear to be to the left of the Sun so, when the Sun sets in the west, Venus would be seen for some time after sunset above the western horizon as an evening star.  In a similar way, if Venus were at a point somewhere on the semicircle ADC, say at D, it would appear from Earth to be to the right of the Sun and it would therefore appear above the eastern horizon just before sunrise as a morning star.

We now know, thanks to the work of Copernicus, that both Earth and Venus orbit the Sun, as do all of the planets in our solar system.  According to the Copernican hypothesis, the reason that Venus sometimes appears as an evening star and sometimes as a morning star can be explained with the aid of diagram 2 below:

venus2 mod

The average distance of Venus from the Sun is 108 million Km. while the average distance of Earth from the Sun is 150 million Km.  Because the circumference of the orbit of Venus is smaller than that of the Earth, we can safely assume that Venus takes less time to complete its orbit than the Earth does. Whereas the Earth moves through 360o in 365.25 days, Venus completes its orbit in 225 days.  For this reason Venus gains 0.6o per day on the Earth and overtakes it at intervals of approximately 600 days.

From the diagram it will be seen that, after Venus has overtaken the Earth (that is after it has passed the point V) it becomes a morning star.  It increases its angular distance to the right of the Sun until it reaches 44o at point X.  After passing X, the angular distance to the right of the Sun decreases until it reaches point Z, which is behind the Sun.  After passing Z, it makes its appearance to the left of the Sun and is now an evening star.  As it approaches Y, its angular distance left of the Sun increases until it reaches 44 o at point Y.  After passing Y on its way to V, its angular distance left of the Sun decreases until, at V, it is zero when it will pass either slightly above or below the Sun.  On extremely rare occasions, it crosses in front of the Sun and this is known as a ‘transit of the planet’.

To sum up, Venus overtakes the Earth at intervals of approximately 600 days.  During approximately 300 of these days, it is a morning star and for the other 300 days, it is an evening star.  The maximum angular distance right or left of the Sun, is roughly 44o.

What about Mercury?  Venus is important to navigators because it is a ‘navigation planet’. (Only those planets that are sufficiently prominent to be observed with an ordinary sextant are considered to be ‘navigation planets; they are Venus, Mars, Jupiter and Saturn).  Even though it is not a ‘navigation planet’, it is interesting to note that Mercury is also an evening and a morning star for similar reasons that Venus is.    Mercury is the closest planet to the Sun and because it has the most elliptical orbit, its distance from the Sun ranges from 29 million Km. to 47 million Km.  Because the circumference of its orbit is comparatively small, it gains 3o on the Earth per day and overtakes it on average every 120 days.  For 60 of these days it will be a morning star and for the other 60 it will be an evening star.  Its maximum angular distance left or right of the Sun is roughly 24o.

So Venus and Mercury are both morning stars and evening stars but it is quite easy to tell them apart for the following reasons: Venus usually appears much higher in the sky than Mercury and is far brighter; in fact, Venus is the third brightest object in the sky after the Sun and the Moon.

In-depth coverage of this and similar topics can be found in the book Astro Navigation Demystified.

w:  www.astronavigationdemystified.com

Posted in Uncategorized | Tagged , , , | Leave a comment

How To Make A Survival Sundial

Posted on May 8, 2013 by Jack Case

Calculating Time In A Survival Situation  

      How To Make A Sundial

Relevant  Links:   Astro Navigation in a Survival Situation, Equation of Time ,  Sidereal Time

Suppose you are shipwrecked on the Skeleton Coast of Namibia or you are a survivor of an aircraft crash in the middle of the Sahara Desert; how would you tell the time?  Simple; look at your watch, you might say; all well and good if you have a watch which is in working order but the chances are that watches and other time pieces would be damaged in shipwreck and air crash situations. Even if they weren’t damaged, they would most probably be set to the standard time of the aircraft’s departure point or the zone time kept by the shipwrecked vessel whereas what we are interested in is the time at our actual position on the Earth’s surface.  You might also say “why do I need to know the time?  All I am interested in is whether it is night or day.  Well suppose for example, you want to hunt for food or look for help; you will want to know how long you have got till sunset so that you can plan your trip to get back to camp before it gets dark.  One way of keeping track of time is to make a sundial.  To do this, we need no equipment other than a few sticks and stones.

At this point it might be useful to consider what we mean by time.  Those who would like to do this, may find this link useful: The Sun as a Time-Keeper.

Making the Survival Sundial.   To be able to construct the survival sundial you will need a rough idea of the latitude of your position.  Obviously, this will be difficult in a survival situation but only an approximate figure is necessary.  For example, returning to the scenario given above, if you are in the Sahara Desert, your latitude will be in the region of 25o north and if you are somewhere in the Namibia Desert, it will be around 22o south.

  1. If we place a stick vertically in the ground, the Sun will cast a shadow from the base of the stick.  At local noon, when the sun is at its highest point in the sky, the shadow will run from north to south (i.e. along the meridian of longitude running through our position).  Place a stone at the other end of this shadow and mark out the line between the stone and the stick.  This will be the noon line.
  2. Next, tilt the stick, in the direction of the shadow so that the angle between the ground and the stick is equal to the approximate latitude in degrees.
  3. The next task is to mark out lines either side of the noon line to indicate the number of hours before or after noon.  To accurately calculate the angle between adjacent hour lines involves trigonometry but it is highly unlikely that you will have a scientific calculator or a set of trigonometry tables in a survival situation; so what we need is a rough ‘rule of thumb’ method. (The formula for accurately calculating the angle is explained at the bottom of the page).
  4. ‘The rule of thumb’ method is that the angle between adjacent hour lines (ao in the diagrams below) will be equal to one quarter of the value of your latitude in degrees.
  5. Next, mark out lines either side of the noon line at the angle calculated above and mark the ends of these lines with stones.   When the Sun’s shadow coincides with either of these lines, the local time will be 1 hour either before or after noon.  Continue in this way until you have 8 lines either side of the noon line.  If, in the morning, the Sun’s shadow coincides with the eighth line to the west of the noon line then the local time will obviously be 8 hours before noon (i.e. 4a.m.) and when it coincides with the third line to the east of the noonline, it will be 3p.m.
  6. The first diagram below illustrates a sundial for latitudes north of 23.5o north.  At latitudes south of 23.5o south, the direction of the Sun at noon will be north instead of south and so the layout of the sundial will be a mirror image of the first diagram (as shown in the second diagram).
  7. In the tropics, i.e. at latitudes between 23.5o north (the Tropic of Cancer) and 23.5o south (the Tropic of Capricorn) the direction of the Sun at noon will sometimes be north and sometimes it will be south.  This will depend on the declination of the Sun as well as the latitude of the observer (click here to see the Survival Declination Table).

For example, on 12th. May, declination is 18.0o north, so at latitude 5.1o north, the direction of the Sun will be due north at noon and the noon shadow will be due south from the stick.  However, on 7th. November at the same latitude, declination will be 11.1o south and so the direction of the Sun at noon will be due south and the noon shadow will be due north.  If the direction of the Sun is south, the sundial should be laid out as shown in the first diagram and if it is north, the second diagram should be used.

We can easily become disoriented in a survival situation and at first, we might not know if the direction of the noon sun is north or south.  However, if we remember that the Sun rises in the East and sets in the west, we can easily align ourselves with north and south.

Accuracy.  Because, in a survival situation, we may not be sure of our latitude and because of the difficulty of calculating and measuring angles, we must appreciate that a sundial such as described above will not be entirely accurate.  However, trials have indicated that an accuracy of ± 15 minutes can be expected and in a scenario such as the one described above, this is considered to be acceptable.

sundial north mod

sundial south mod

On 5th. April, the declination will be 5.1o north and so the Sun will be directly overhead at noon at latitude 5.1o north.  In this situation of course, there will be no shadow from the stick and so it will not be possible to mark the north/south line.  However, at latitudes close to the Equator, there may be another way of making the sundial. We know that within a few degrees of the Equator, the Sun rises at 06.00 and sets at 18.00 to within a few minutes of accuracy.  So, marking the stick’s shadow at sunrise and then marking out the hourly increments from there, may enable us to solve the problem.

Formula to calculate angle between adjacent hour markers on dial of sundial:

                            tan a = sin L . tan s

Where a = angle between adjacent hour markers

L = latitude

s = angular distance moved by the Sun in 1 hour (ie. 15o)

Example. To calculate angle between adjacent hour markers at latitude 50o.61:

tan a = sin(50o.61) . tan (15o)

= 0.773 x 0.268

Tan a-1 = 11.695o

The object used to cast the shadow (in this case, a stick) is known as a gnomon.  The angle between dial and gnomon is equal to latitude of observer.  Therefore, at 50o.61 north, the angle between the ground and the gnomon = 50o.61.

A comprehensive exposition of this topic can be found in the book Astro Navigation Demystified.

Survival Topics Links:

Astro Navigation in a Survival Situation

The Sun as a Time-Keeper

The Equation of Time

Local Hour Angle

North/South Movement of the Sun.

Declination

Declination Table

Sidereal Time

www.astronavigationdemystified.com

Posted in Uncategorized | Tagged , , , , , , | Leave a comment

What Is Sidereal Time

Posted on April 14, 2013 by Jack Case

Sidereal Time.  Even though Sidereal Time is a more accurate measure of the Earth’s rotation, we normally use Solar Time for time-keeping because the Sidereal Day is not a practical unit for us to use.  On the other hand, Sidereal Time is important because it enables us to find the hour angle of a star and is therefore essential if we wish to use stars for navigation.

Solar Day.  A Solar Day is the time interval between two successive transits by the Sun across the meridian directly opposite that of the observer; that is the 24 hour interval from midnight to the following midnight at the observer’s meridian.

Sidereal Day.  A Sidereal Day is the interval between two successive transits of a star across the observer’s meridian.  A Sidereal Day is shorter that a Solar Day by approximately 4 minutes and is a true measure of the period of rotation of the Earth. For convenience, the First Point of Aries is used to mark the Sidereal Day instead of an actual star.  The Sidereal Day is therefore defined as the interval between two successive transits of the First Point of Aries across the same meridian.  The Sidereal Day begins when the First Point of Aries crosses the meridian.

Local Sidereal Time is equal to the Local Hour Angle of the First Point of Aries.  This is abbreviated to Local Sidereal Time = LHA of Aries. 

First Point of Aries.  In astronomy, we need a celestial coordinate systems for fixing the positions of all celestial bodies in the celestial sphere.  To this end, we express a celestial body’s position in the celestial sphere in relation to its angular distances from the Celestial Equator and the celestial meridian that passes through the ‘First Point of Aries’.   This is similar to the way in which we use latitude and longitude to identify a position on the Earth’s surface in relation to its angular distances from the Equator and the Greenwich Meridian.  The First Point of Aries is usually represented by the ‘ram’s horn’ symbol shown below:

aries

Just as the Greenwich meridian has been arbitrarily chosen as the zero point for measuring longitude on the surface of the Earth, the first point of Aries has been chosen as the zero point in the celestial sphere.  It is the point at which the Sun crosses the celestial equator moving from south to north (at the vernal Equinox in other words).

So the First Point of Aries is the starting point of the Solar Year and it is also the starting point of the Sidereal Day.

The confusing thing about the First Point of Aries is that, although it was in the constellation of Aries when it was chosen by the ancient astronomers, due to precession it now lies in Pisces.

Hour angles explained:

Local Hour Angle (LHA). In astro navigation, we need to know the position of a celestial body relative to our own position.  In the diagram below:

diag3

LHA is the angle BNU on the Earth’s surface which corresponds to the angle ZPX in the Celestial sphere. In other words, it is the angle between the meridian of the observer and the meridian of the geographical position of the celestial body (GP).

Due to the Earth’s rotation, the Sun moves through 15o of longitude in 1 hour and it moves through 15 minutes of arc in 1 minute of time. So the angle ZPX can be measured in terms of time and for this reason, it is known as the Local Hour Angle.

LHA is measured westwards from the observer’s meridian and can be expressed in terms of either angular distance or time. For example, at noon (GMT) the Sun’s GP will be on the Greenwich Meridian (0o). If the time at an observer’s position is 2 hours and 3 minutes after noon, then the angular distance between the observer’s meridian of longitude and the Greenwich Meridian must be (2 x15o ) + (3x 15’) = 30o 45’. Because it is after noon at the observer’s position, the longitude of that position must be to the East of the Greenwich Meridian since the Earth rotates from West to East. Therefore the observer’s longitude must be 30o 45’ East and since LHA is measured westwards from the observer’s meridian, the LHA must also be 30o 45’. However, it should be noted that as the Earth continues to rotate eastwards, the GP of the Sun will continue to move westwards so the LHA at the observer’s position will be continually changing.

Greenwich Hour Angle (GHA). As discussed above, the angle between two meridians of Longitude can be expressed as an hour angle. The hour angle between the Greenwich Meridian and the meridian of a celestial body is known as the Greenwich Hour Angle.

The Local Hour Angle between an observer’s position and the geographical position of a celestial body can be found by combining the observer’s longitude with the GHA.

Sidereal Hour Angle (SHA). SHA is the angle between the meridian running through the First Point of Aries and the meridian running through the celestial body measured westwards from Aries. The Nautical Almanac does not list the GHA of the stars; it lists their sidereal hour angle (SHA) instead. So, the GHA of a star has to be calculated from the GHA of Aries. Therefore, the SHA of the star must be added to the GHA of Aries in order to obtain the GHA of the star.

Relevant links:

Time Difference Between Meridians of Longitude

Find Your Longitude in a Survival Situation

Equation of Time

Survival Sundial

A comprehensive exposition of this topic can be found in the book Astro Navigation Demystified.

www.astronavigationdemystified.com

Posted in Uncategorized | Tagged , , , , , | 3 Comments

What Is The Equation of Time

Posted on April 6, 2013 by Jack Case

The Sun as a Time-Keeper.  Because the Earth’s orbital motion is not uniform, there are corresponding variations in the apparent speed of the Sun as it travels round the earth.   For this reason, the true Sun (the Sun that we see in the sky) does not give an accurate measurement of time and to overcome this problem, the Mean Sun, as defined below, is used.

The Mean Sun is an imaginary body which is assumed to move at a uniform speed round the Earth thereby giving a uniform progression of time.

Solar Time.  The true sun gives us apparent solar time while the mean sun gives us mean solar time.

The Equation of Time.  To enable us to connect mean solar time with apparent solar time, we have the Equation of Time which is defined as follows:

Equation of Time = mean solar time – apparent solar time

In other words, the equation of time is the difference between apparent solar time and mean solar time taken at the same instant at one place.

Example.  An observation of the Sun is made at 11h 05m 22s GMT on 26August 2009.  What is the apparent solar time?

The Eqn. of Time on that date is -01m 55s.

Eqn. of Time = mean solar time – apparent solar time.

so apparent solar time = mean solar time – Eqn. of Time.

= 11h 05m 22s – (-)01m 55s

Therefore, apparent solar time = 11h 07m 17s

Notes.

  • The equation of time can be either positive or negative depending on the time of the year.
  • The values range from approximately +15 to -15 mins.
  • The values are positive from 15th April to 14th June and from 1st  September to 24th December.
  • The values are negative from 15th June to 31st August and from 25th December to 14th April.

The following chart illustrates this information.

eotmark2

Tables which accurately show the equation of time for each day of the year can be found in the various versions of the nautical almanac and also on the Internet.

Relevant links:  

The Survival Sundial

Sidereal Time

Time Difference Between Meridians of Longitude

A comprehensive exposition of this subject can be found in the following book:  Astro Navigation Demystified.

www.astronavigationdemystified.com

Posted in Uncategorized | Tagged , , , , , | 1 Comment

What Is The Mason Dixon Line

Posted on September 25, 2012 by Jack Case

Astro Navigation and the Mason Dixon Line

Between 1763 and 1768, about 200 years before the advent of GPS, Charles Mason and Jeremiah Dixon marked the 233 mile long boundary line between Pennsylvania and Maryland and the 83 mile long boundary between Maryland and Delaware; this was the Mason-Dixon Line.

When cartographers such as Samuel De Champlain and James Cook plotted the coastlines of North America in the fifteenth and sixteenth centuries respectively, they would have used instruments such as the astrolabe and the sextant to measure the altitudes of celestial bodies in relation to the horizon.  Such instruments would have been of little use to Mason and Dixon amongst the forests and hills of Delaware and Pennsylvania where the horizon would not be visible so, instead of measuring the altitudes of celestial bodies, they used a device called a ‘zenith sector’ to measure the zenith distance, that is the angle between their zenith and the celestial body.

In the diagram below, B is the position of an observer on the Earth’s surface and Z is the observer’s zenith.                                                                                                                               X is the position of a celestial body and U is the geographical position of the body on the Earth’s surface.                                                                                                                                BH is the visible horizon from B.                                                                                              Angle XBH is the altitude and angle XBZ is the zenith distance (90o – altitude).

The zenith sector is a far more accurate instrument for measuring angles than the sextant for several reasons:

  • Firstly, whereas the sextant is a hand-held instrument which is used from the pitching deck of a ship, the zenith sector is a fixed instrument which is placed on solid ground.
  • Secondly, whereas a sextant with a vernier scale allows you to measure angles to an accuracy of 0.1 minutes of arc, it is possible to achieve an accuracy of 0.1 seconds of arc with a zenith sector.
  • Thirdly, refraction is at a minimum when a celestial body nears its zenith and so the accuracy of the zenith sector which measures the angle between the observer’s zenith and the body when it is at its zenith, will be less affected by refraction.  On the other hand, when a sextant is used to measure the altitude of bodies closer to the horizon where refraction is greatest, a correction has to be made.
  • Fourthly, a sextant is used to measure the angle between the body and the horizon.  As shown in the diagram below, the observer measures the altitude in relation to the visible horizon from his position at O on the Earth’s surface.  So, the observed altitude is the angle HOX.  However, the true altitude is measured from the Earth’s centre in relation to the celestial horizon and is the angle RCX.

Point O will be approximately 6367 Km. from the centre of the Earth and so it would seem that the visible horizon is bound to be slightly offset from the celestial horizon.  Because of the vast distances of the stars and the planets from the Earth, we can assume that, in their cases, the celestial horizon and the visible horizon correspond with very little error.  However, in the cases of the Sun and the Moon, which are relatively near, a correction called Parallax must be added.

  • Finally, when using a sextant, a correction has to be made to allow for the height of the observer’s eye above the horizon, this is known as Dip.  Consider the diagram below:

In the diagram, O is an observer’s position on the Earth’s surface and E is the position of his eye.  We can see that, as the observer’s height of eye is raised above sea level, his visible horizon ‘dips’ below the true horizon and so the altitude measured at E becomes greater than that measured at O.

Dip is the error caused by this difference and has to be subtracted from the reading.

The method used by Mason and Dixon to calculate latitude.  To an observer on the Earth’s surface, a celestial body will rise in the east, ascend until it reaches its zenith and then descend until it sets in the west.  When the body reaches its zenith in relation to the observer, it will be over the observer’s meridian of longitude.  If, at that moment, the observer were to measure the angular distance from his zenith to the celestial body, he will have measured its zenith distance.  Since the body is over the observer’s meridian, its bearing will be either north or south (unless of course it is overhead).

The Declination of a celestial body can be summarised as the celestial equivalent of Latitude since it is the angular distance of a celestial body North or South of the Celestial Equator.

Say, for example, we calculate that a star’s zenith distance is 5o 15’ while its bearing is due south, we can conclude that our latitude is 5o 15’ north of the star’s declination.  If the declination of the star is 39o 30’ North, then our latitude must be 39o 30’ + 5o 15’, that is 44o 45’ north.  This in essence is the method used by Mason and Dixon when using a zenith sector to calculate latitude.

The reason that they chose to use stars for their observations is that the declinations of the stars change very slowly and can be considered to be almost constant for up to a month at a time.  The declinations of the Sun, the Moon and the planets change rapidly in comparison with the stars and to use these celestial bodies would have made their calculations more complicated.

Calculating latitude from the altititude of the Sun.  If you wish to learn about the method used at sea to find your latitude from the altitude of the Sun at midday, click here.

Definitions:

Zenith. The point on the celestial sphere directly above the observer is called the Zenith. The term zenith is also used to refer to the highest point reached by a celestial body during its apparent orbit around a given point of observation.

The altitude is the angle between the celestial horizon and the direction of the celestial body.

The celestial horizon is the projection of the observer’s horizon onto the celestial sphere.

The zenith distance is the angle between the direction of the celestial body and the observer’s zenith.

Declination.  The Declination of a celestial body is its angular distance North or South of the Celestial Equator.

For further information visit www.astronavigationdemystified.com

Posted in astro navigation | Tagged , , , , | Leave a comment

How To Locate The Pole Star (Polaris)

Posted on August 29, 2012 by Jack Case

First step – Look in the northern sky to find the constellation Ursa Major which is otherwise known as the Great Bear.

Second step – find the Big Dipper (marked in red) which consists of the seven brightest stars of the constellation Ursa Major.  The alternative name for the Big Dipper is the Plough

Third step – In the diagram below, follow the imaginary arrow from the Big Dipper and you will find that it points to the brightest star in the group of stars known as Ursa Minor which is alternatively known as the Little Dipper or the Little Bear. The star to which the arrow points is known as Polaris or the Pole Star.

Finding your latitude from the Pole Star

www.astronavigationdemystified.com

Posted in Astro Navigation Topics, navigation, Schools, Survival | Tagged , , , , , | 4 Comments

The Southern Cross

Posted on August 29, 2012 by Jack Case

Just as we can use the Pole Star in the northern hemisphere to find the direction of north, we can use the Southern Cross in the southern hemisphere to find the direction of south.   However, whereas we can use the Pole Star to calculate our latitude, the Southern Cross is too far removed from the south celestial pole to be of any use for that purpose.

The Southern Cross,  or Crux, is one of the best known constellations in the southern hemisphere, and is easily recognizable for the cross-shaped asterism formed by its four brightest stars. Crux (Latin for cross) is not visible north of +20° in the northern hemisphere but it is circumpolar south of 34° in the southern hemisphere which means that it never sets below the horizon there.

The cross  has four main stars marking the tips (alpha, beta, gamma and delta).

Alpha Crucis is also known as Acrux (a contraction of ‘alpha’ and ‘Crux’).  This is the brightest star in the constellation Crux.

Beta Crucis, also known as Mimosa or Becrux is the second brightest star in the constellation.

Gamma Crucis or Gacrux, is the third brightest star in Crux.

Delta Crucis or Palida is the fourth star and has variable levels of brightness .

The Pointers.  The constellation Centaurus contains two bright stars: alpha Centauri also known as Rigil Kentaurus and beta Centauri also known as Hadar, which we use as pointers to the Southern Cross.

How to find the direction of south by using the Southern Cross.  There are several methods of doing this but the simplest is as follows

  1. Make an imaginary line between Gacrux and Acrux.
  2. Extend this line from Acrux (the brightest star) for 4.5 times the length of the Southern Cross, as shown in the diagram below.  This will take you to the position of the South Celestial Pole in the sky.
  3. From the South Celestial Pole, drop a line down to the horizon.  Where this line touches the horizon is the direction of south.

HOME

 

Links:  Locating Polaris   Latitude from Polaris   Astro Navigation for Survival

Astro Navigation Demystified

Posted in Astro Navigation Topics, navigation, Survival | Tagged , , , , , , , , , | 1 Comment

The Rhumb Line

Posted on August 29, 2012 by Jack Case

If a ship were to steer a steady course, that is one on which her heading remains constant, her track would cut all meridians at the same angle, as the following diagram shows.  Such a line on the Earth’s surface is called a rhumb line.

When the rhumb line cuts all meridians at 90o, it will coincide with either a parallel of latitude or with the Equator.  When the angle is 0o, the rhumb line will be along a meridian of longitude.  A vessel’s course will always be a rhumb line; thus the course to be steered to travel from one place to another will refer to the angle between the rhumb line joining the places and any meridian.

 Calculating the distance between two points along a rhumb line. In the next diagram, A, B, C, D and Z are meridians of longitude;  the lines aB, bC, and cD are different parallels of latitude; and the line ABCDZ is a rhumb line.  A series of right-angled triangles have been constructed along the rhumb line AZ and in each triangle, one short side lies along a meridian of longitude, one lies along a parallel of latitude and the hypotenuse lies along the rhumb line.

It can be seen from the diagram that the east-west distance between two points along the rhumb line is the sum of the distances along the parallels of latitude corresponding to the difference in longitude in each of the right-angled triangles.  This east-west distance is known as the departure

Middle Latitude. If we were to calculate the departure along each of the parallels of latitude aB, bC, cD, in the diagram above, we would find that they would not be equal and so the task of calculating the total departure would be complicated.  In practice, the total departure is taken to be the east-west distance along the intermediate of these parallels which is known as the ‘middle latitude’.

The formula to calculate departure is as follows:

Departure = d.long cos(middle latitude).

Mean Latitude.  In most cases, the arithmetic mean of the two latitudes can be used as the middle latitude without appreciable error, so the approximate formula dep.= d.long cos(mean lat) may be used.

When the difference of latitude is large (over 600 n.m.) or the latitudes are close to either of the poles, the middle latitude must be used instead of the mean latitude and in these cases, we have the more accurate formula:

Dep. = d.long cos(mid lat).

 The difficulty lies in the task of calculating the middle latitude which involves finding the mean of the secants all the intermediate latitudes by integration.  Such methods are obviously impracticable in situations where courses and distances have to be calculated rapidly at sea.  For this reason, tables of corrections to be applied to the mean latitude are contained in various collections of nautical tables.  Since, astro navigation involves short distance sailing calculations, it is not intended to copy middle latitude correction tables here; however, the following example demonstrates their use:

Suppose a ship sails from position 50oN, 32oE., to 70oN., 15oE.  The d.long is 17o and the mean latitude is 60o.

The formula for calculating departure using the mean lat. is:

dep.= d.long cos(mean lat)

Using this formula we have:

Dep. = 17o cos(60)

= 1020’ cos(60)

= 510’ or 510 n.m.

In the tables for converting mean latitude to middle latitude, the correction for a mean latitude of 60o and a difference of latitude of 20o is +1o 09’.  So the middle latitude = 61o.15.

The formula for calculating departure using the middle latitude is:

Dep. = d.long cos(mid lat).

= 1020 cos (61.15)

= 492.17 n.m.

By comparing these results, we can see that there is a significant difference between calculations involving the mean latitude on one hand and the middle latitude on the other.

Summary of Formulae.  The formulae so far derived are summarised below:

Ddist  =  Dlong x Cos Lat.

Dlong  =   Ddist ÷ Cos Lat. = Ddist x Sec Lat.

dep.= d.long cos(mean lat) (for distances 600 n.m. or less).

Dep. = d.long cos(mid lat). (for distances over 600 n.m.).

 The Rhumb Line Formulae.

With the next diagram, we expand on the work above,

  • The rhumb line AZ is divided into a large number of equal parts AB, BC, CD, DZ.
  • aB, bC, cD… are arcs of parallels of latitude drawn through B, C, D…..
  • Pa’, Pb’, Pc’… are meridians of longitude.
  • Therefore, the angles at a, b, c….. are right angles.

If the divisions of AZ are made sufficiently small, the triangles ABa, BCb, CDc…..  will be small enough to be treated as plane triangles instead of spherical triangles.

  • Since the course angle is constant by the definition of a rhumb line, these small triangles are equal.

Consider triangle ABa in the diagram;

AB is the distance made good, aB is the departure along a parallel of latitude, angle aAB is the course angle.

Therefore, Sin(course angle) = departure ÷ dist.  This formula applies to all of the small triangles since they are equal.

By transposition, the above formula becomes:

Dep = Dist x sin(course)

The departure between A and Z therefore, is the sum of the departures of all of the small triangles.

Therefore, by addition:

aB + bC + cD + …. = (AB + BC + CD + …. x sin(course)

i.e. Dep = Dist sin(course) 

If we again consider triangle ABa,  Aa = AB cos (course)

But Aa is the difference in Latitude (D.Lat) between A and B

So D.Lat = AB cos(course)

Again, this formula applies to all of the small triangles since they are equal.  Therefore, by addition, the total D.Lat corresponding to the total distance between A and Z becomes:

D.Lat = Dist cos(course)

We have established formulae to calculate Dep and D.Lat; we now need a formula to find the course.

If we return to triangle ABa, we can see that the course angle can be found by the formula:  tan(course) = Dep ÷ D.Lat.

As before, this formula applies to all of the small equal triangles.  So, by addition, the rhumb line course between A and Z can be found by the formula:

Tan(course) = Dep ÷ D.Lat  

Short Distance Sailing.

Short distance sailing is a term which is applied to sailing along a rhumb-line for distances less than 600 nautical miles.  From the formulae derived in this chapter, the following are used extensively in short distance sailing:

To Calculate Departure when the course is not known:

dep.= d.long cos(mean lat)

To Calculate Departure when the course is Known:

Dep  = Dist x Sin(course)

To Calculate Distance when departure and course are known:

Dist  =         Dep  ÷ Sin (course)

To Calculate Dlat when the distance and course are known:

DLat = Dist x Cos(course)

To Calculate Course to Steer(the rhumb line course between two points)

Tan(course) =   Dep  ÷ D.Lat

To calculate Dlong (difference in longitude corresponding to the departure):

DLong.  =  Dep. x Sec(Mean.Lat)   or Dlong =      Dep ÷ Cos(Mean.Lat)

Example.  At 0900 GMT, a life raft is reported to be in position 30o 56’.4 S, 0o 25’.6 E.  A rescue ship reports that its ETA at the vicinity is 2130 GMT.  The rescue ship’s navigator calculates that wind and ocean currents will cause the life raft to drift in direction 345o at 3 knots.  Calculate the expected position of the life raft when the rescue ship is due to arrive.

Solution:

Time taken for rescue ship to reach reported position of life raft = 12.5 hours.Distance that raft is expected to drift in direction 345o in that time = 37.5 n.m.Therefore Dist. = 37.5 n.m.Dep. = 37.5 Sin(345) = 9’.7 WestDlat = 37.5 Cos(345) = 36’.2N

New Lat    = 30o 20’.2S.

M.lat           = 30o 38’.3S.

DLong.      = 9.7 Sec(30.64) = 11’.27W.

New Long   = 0o 14’.33E

Therefore, expected position of raft at 2130  = 30o 20’.2S.  0o 14’.33E   

 A fuller explanation of rhumb line sailing together with the derivation of the formulas given above can be found in the book ‘Astro Navigation Demystified’.

Link: The relationships between longitude and latitude and the nautical mile

web: www.astronavigationdemystified.com 

email: bookcase.learning@btinternet.com

 

Posted in astro navigation, navigation | Tagged , , , , | 1 Comment

The Relationship Between Longitude, Latitude and the Nautical Mile.

Posted on August 29, 2012 by Jack Case

The Relationship Between Longitude and the Nautical Mile.  The Earth’s equatorial circumference is 21640.6 n.m.  Since the Equator is a great circle, 1o will subtend an arc of:  21640.6 ÷ 360 =  60.113  ≈ 60 n.m.

There are 360 meridians of Longitude so it follows that, measuring from the Earth’s centre, the angular distance between adjacent meridians at the Equator is 1o.  Since, as calculated above, 1o subtends an arc of 60 n.m. it follows that the distance between adjacent meridians of longitude at the Equator is 60 n.m.

The angular difference between longitude 10o West and the Greenwich Meridian is 10o; therefore, the distance between them at the Equator is 10 x 60 = 600 n.m.

The Relationship between Latitude and the Nautical Mile.  The Earth’s meridional circumference is calculated to be 40007.86 Km. which equates to 21604.2 nautical miles (n.m.).  In other words, an angle of 360o at the Earth’s centre subtends an arc of 21604.2  n.m. on the  surface of a meridian of Longitude which is by definition a great circle.

From the above, it follows that 1o measured along a meridian of longitude, will subtend an arc of:  21604.2 ÷ 360 =  60.012  ≈  60 n.m.  and 1′ will subtend an arc of: 60 ÷ 60  =  1 n.m

As calculated above, an angle of 1o at the Earth’s centre will subtend an arc of 60 n.m. along a meridian of longitude.  Therefore, any point on the parallel of latitude 1o North will have an angular distance of 60 n.m. north of the Equator.

The angular distance between latitude 62o.8 N. and latitude 48o.5 N. is 14o.3.  Therefore, the distance between these lines of latitude measuring due north or south along a meridian of longitude will be: 14.3 x 60 = 858 n.m.

Measuring the Distance Between Meridians of Longitude Along a Parallel of Latitude.  We know that the distance between adjacent meridians of longitude at the Equator is 60 n.m.  This is because the Equator is a great circle; parallels of latitude however, are small circles and this presents us with a problem.  In the diagram,  PBC and PAD lie on separate meridians of longitude.

The arc BA is the distance between these meridians measured along a certain line of latitude.  The arc CD is the distance between the same meridians measured along the Equator.  Clearly, the distance CD is much greater than the distance BA.

The following formulas are used for calculating the difference in distance along a parallel of latitude (Ddist) corresponding to a difference in longitude (Dlong) and vice versa.  (The formulas are simply stated below without explanation but a full explanation of their derivation is given in the book ‘Astro Navigation Demystified’).

 Ddist = Dlong x Cos Lat.   and  Dlong = Ddist ÷  Cos Lat.

Since the secant is the inverse of the cosine, the formula for Dlong can be simplified to:  Dlong = Ddist x Sec Lat.

To learn about the application of these formulas visit this page: The Rhumb Line

web:  www.astronavigationdemystified.com

email: bookcase.learning@btinternet.com

Posted in Astro Navigation Topics, navigation | Tagged , , , , , , , , , , , | Leave a comment