If we were to measure the altitude and the bearing of the Sun at our position on the Earth’s surface, we would find that the maximum altitude during the course of a day occurs at noon when the Sun lies directly over our meridian of longitude and therefore bears north or south. We can use this fact to calculate our latitude.
The following diagrams will help to explain how the latitude can be calculated from the Sun’s midday altitude and its declination.
In the following diagram ,
NOS represents the horizon and O represents the position of the observer,
X represents the position of the Sun,
Z represents an imaginary position exactly above the observer so that OZ is perpendicular to NOS,
OX represents a line from the observer to the Sun,
angle XOS represents the altitude of the Sun at midday,
angle XOZ equals 90o – Altitude.
Now consider the next diagram.
Imagine the Earth to be at the centre of the imaginary celestial sphere with the positions Z and X projected onto the surface of that sphere.
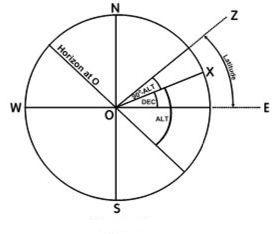WOE represents the projection of the Equator onto the surface of the sphere,
NOS represents the projection of a line joining the North and South poles onto the surface of the sphere.
angle EOZ equals the latitude of the observer,
angle EOX equals the declination of the Sun,
angle XOZ equals 90o – Altitude
Therefore, Lat. = Declination + (90o-Altitude).
In the case above, latitude and declination are in the same hemisphere but the latitude is greater than the declination. There are two other cases to consider:
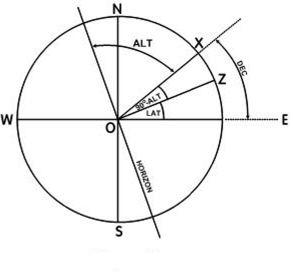
In the next diagram, latitude and declination are in the same hemisphere but declination is greater than latitude.
In this case:
Declination = (90o – Altitude) + Latitude
therefore Lat. = Dec. – (90o – Alt.)
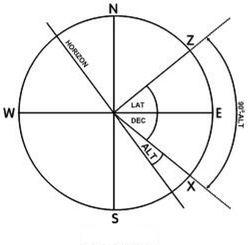
In the next case, latitude and declination are in opposite hemispheres as shown in this diagram:
In this case:
Latitude + Declination = (90o – Altitude)
therefore, Lat. = (90o – Alt.) – Dec.
We can summarise the rules for the three cases as follows:
(i) Latitude and declination same names and latitude greater than declination:
LAT = DEC + (90o – ALT)
(ii) Latitude and declination same names and declination greater than latitude:
LAT = DEC – (90o – ALT)
(iii) Latitude and declination contrary names:
LAT = (90o – ALT) – DEC
Examples:
1. Using rule (i)
Scenario: True altitude at midday: 72o 30’.1 Sun’s declination: 23o 21’.3
LAT = DEC + (90o – ALT) (rule i)
= 23o 21’.3 + (90o – 72o 30’.1)
= 23o 21’.3 + 17o 29’.9
= 40o 51’.2 S.
2. Using rule (ii)
Scenario: True altitude at midday: 69o 41’.3 Sun’s declination: 23o 25’.6
LAT = DEC – (90o – ALT) (rule ii)
= 23o 25’.6 – (90o – 69o 41’.3)
= 23o 25’.6 – 20o 18’.7
= 3o 06’.9 N.
3. Using rule (iii)
Scenario: True altitude at midday: 80o 48’.01 Sun’s declination: 2o 59’.0
LAT = (90o – ALT) – DEC (rule iii)
=(90o – 80o 48’.01) – 2o 59’.0
=9o 11’.99 – 2o 59’.0 =6 o 12’.9N.
A fuller explanation of this topic is given in the book ‘Astro Navigation Demystified’.
Links: Calculating Longitude. Astro Navigation Demystified.
Home page: www.astronavigationdemystified.com
Astro Navigation Demystified 
Pingback: The Mason Dixon Line | Astro Navigation Demystified